set.seed(42)
m2 <-
stan_glm(price ~ 1, data = HousePrices, refresh = 0)7 Gauss-Modelle
Hinweis: Achtung, die Ergebnisse können selbst mit set.seed() etwas variieren!
7.1 Aufgabe 1
Nehmen Sie für folgende Aufgaben den Datensatz mtcars aus dem Paket datasets.
7.1.1 Aufgabe 1 a)
Stellen Sie ein generalisiertes lineares Modell auf, das zeigt, welchen mittleren Spritverbrauch wir zu erwarten haben.
set.seed(42)
m1 <- stan_glm(mpg ~ 1, data = mtcars, refresh = 0)7.1.2 Aufgabe 1 b)
Lassen Sie sich eine Zusammenfassung der Postverteilung ausgeben und geben Sie den Wert an, den das Modell am wahrscheinlichsten für den Mittelwert hält. Geben Sie außerdem einen Bereich an, in dem laut dem Modell zu 95-prozentiger Wahrscheinlichkeit der echte Mittelwert liegt.
parameters(m1)Parameter <chr> | Median <dbl> | CI <dbl> | CI_low <dbl> | CI_high <dbl> | |
|---|---|---|---|---|---|
| (Intercept) | 20.07462 | 0.95 | 17.94755 | 22.25988 |
Der Punktschätzer unseres Modells ist 20, während das Konfidenzintervall, in dem der echte Wert zu 95 Prozent liegt, von 17,95 bis 22,26 geht.
7.1.3 Aufgabe 1 c)
Geben Sie das Modell als Tabelle aus und visualisieren Sie die Verteilungen für den durchschnittlichen Spritverbrauch und die Streuung.
m1tab <-
m1%>%
as_tibble()%>%
rename(mean = `(Intercept)`)- 1
- Optionale Umbenennung der Spalte (Intercept)
ggplot(m1tab, mapping = aes(x = mean))+
geom_density()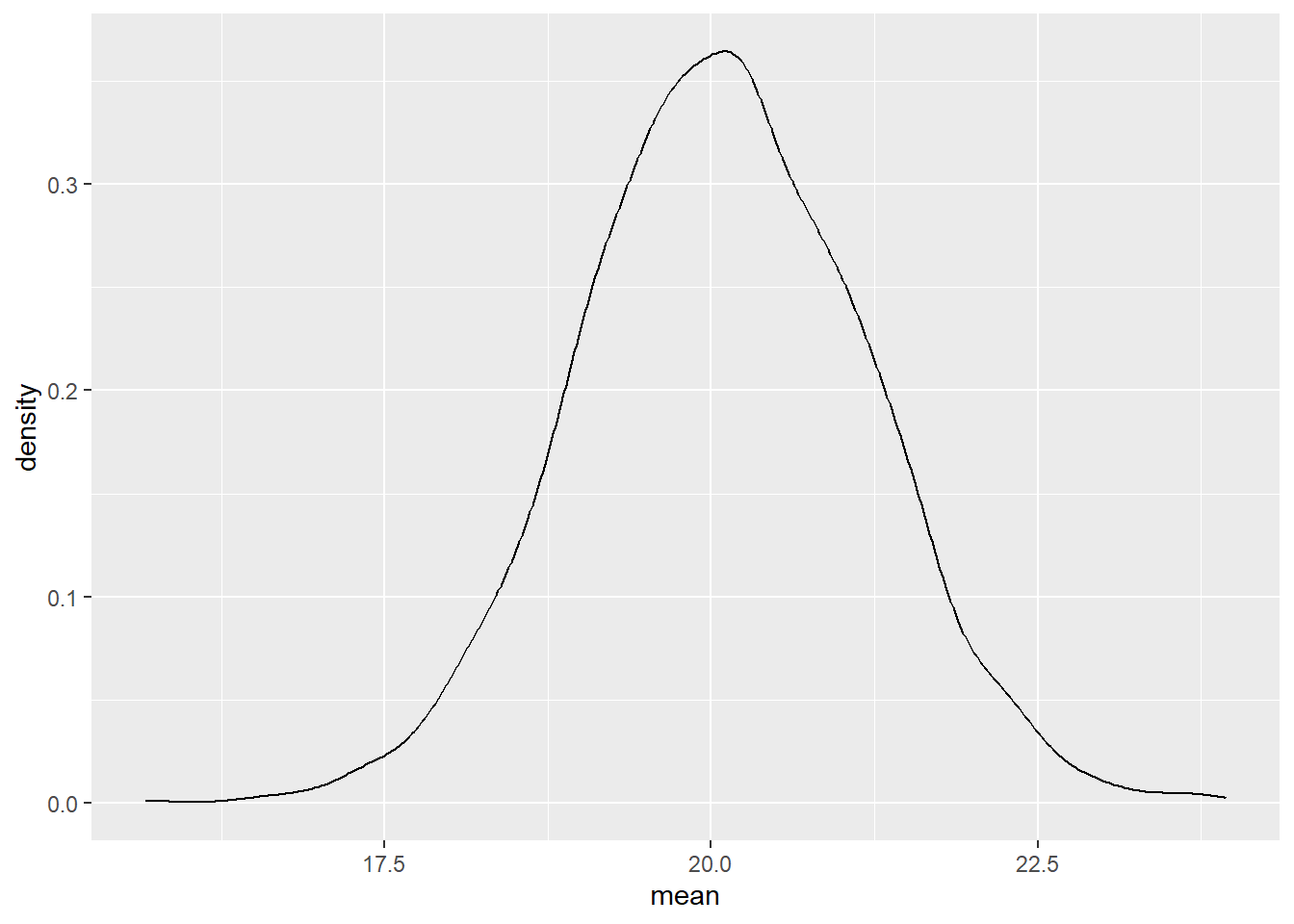
ggplot(m1tab, mapping = aes( x = sigma))+
geom_density()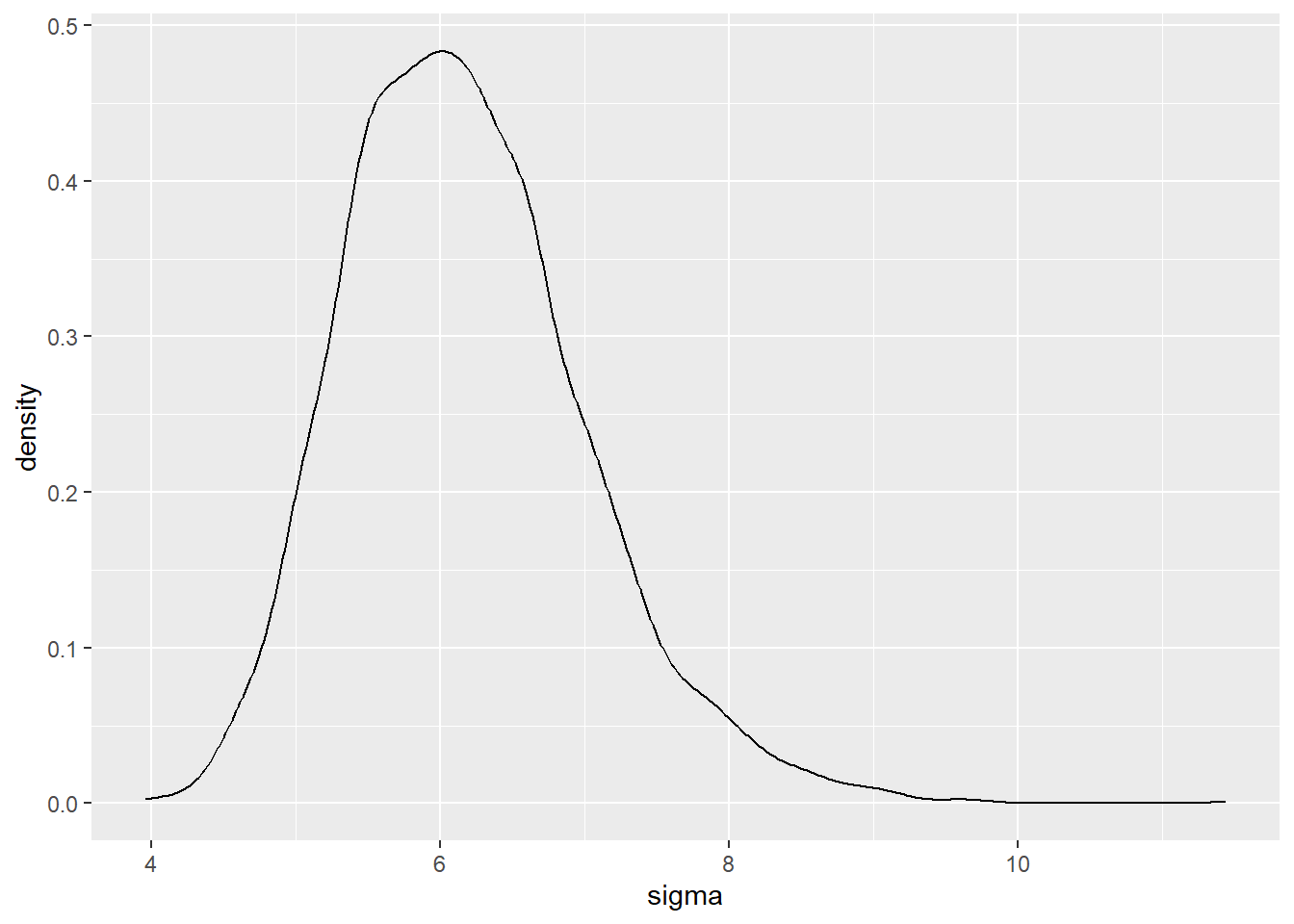
7.1.4 Aufgabe 1 d)
Geben Sie die Wahrscheinlichkeit dafür, dass der mittlere Spritverbrauch nicht größer ist als 21 mpg.
m1tab%>%
count(mean <= 21)%>%
mutate(Anteil = n / sum(n))mean <= 21 <lgl> | n <int> | Anteil <dbl> |
|---|---|---|
| FALSE | 818 | 0.2045 |
| TRUE | 3182 | 0.7955 |
Oder eleganter:
m1tab %>%
summarise(Anteil = mean(mean <= 21))Anteil <dbl> |
|---|
| 0.7955 |
Die Wahrscheinlichkeit, dass der mittlere Spritverbrauch nicht größer ist als 21 mpg, liegt bei ca. 80 Prozent.
7.1.5 Aufgabe 1 e)
Welche Streuung wird mit einer Wahrscheinlichkeit von 90 Prozent nicht überschritten?
m1tab%>%
summarise(quant90 = quantile(sigma, prob = .9))quant90 <dbl> |
|---|
| 7.246123 |
Eine Streuung von 7.25 wird mit einer Wahrscheinlichkeit von 90 Prozent nicht überschritten.
7.1.6 Aufgabe 1 f)
Wie breit ist das Intervall der höchsten Dichte, das angibt in welchem Bereich sich 90 Prozent der möglichen Durchschnittsverbrauche befinden?
m1tab%>%
select(mean)%>%
hdi(ci = .9)Parameter <chr> | CI <dbl> | CI_low <dbl> | CI_high <dbl> |
|---|---|---|---|
| mean | 0.9 | 18.22961 | 21.811 |
21.81 - 18.23[1] 3.58Oder eleganter:
m1tab%>%
select(mean)%>%
hdi(ci = .9) %>%
mutate(width = CI_high - CI_low) %>%
select(width)width <dbl> |
|---|
| 3.581394 |
Die Breite des 90-Prozent-HDIs beträgt 3.58.
7.2 Aufgabe 2
Laden Sie den Datensatz “HousePrices” aus dem gegebenen Archiv:
https://vincentarelbundock.github.io/Rdatasets/datasets.html
Stellen Sie ein Modell auf, das zeigt mit welchem Mittelwert und welcher Streuung im Preis der Häuser zu rechnen ist.
HousePrices <-
read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/AER/HousePrices.csv")7.2.1 Aufgabe 1 b)
Lassen Sie sich eine Zusammenfassung der Postverteilung ausgeben und geben Sie den Wert an, den das Modell am wahrscheinlichsten für den Mittelwert hält. Geben Sie außerdem einen Bereich an, in dem laut dem Modell zu 95-prozentiger Wahrscheinlichkeit der echte Mittelwert liegt.
parameters(m2)Parameter <chr> | Median <dbl> | CI <dbl> | CI_low <dbl> | CI_high <dbl> | |
|---|---|---|---|---|---|
| (Intercept) | 68116.22 | 0.95 | 65952.65 | 70357.75 |
Der Punktschätzer unseres Modells ist 68k, während das Konfidenzintervall, in dem der echte Wert zu 95 Prozent liegt, von 65952.65 bis 70357.75 geht.
7.2.2 Aufgabe 2 c)
Wie groß ist die Wahrscheinlichkeit, dass der durchschnittliche Häuserpreis mehr als 70.000 Dollar ist?
m2tab <-
m2%>%
as_tibble()%>%
rename(mean = `(Intercept)`)m2tab%>%
count(mean > 70000)%>%
mutate(Anteil = n / sum(n))mean > 70000 <lgl> | n <int> | Anteil <dbl> |
|---|---|---|
| FALSE | 3802 | 0.9505 |
| TRUE | 198 | 0.0495 |
Oder eleganter:
m2tab %>%
summarise(Anteil = mean(mean > 70000))Anteil <dbl> |
|---|
| 0.0495 |
Die Wahrscheinlichkeit, dass der mittlere Häuserpreis bei mehr als 70.000 Dollar liegt, ist laut dem Modell lediglich 5 Prozent.
7.2.3 Aufgabe 2 d)
Wie groß ist die Wahrscheinlichkeit, dass die Streuung der Häuserpreise bei 20.000 Dollar oder weniger liegt?
m2tab%>%
count(sigma <= 20000)%>%
mutate(Anteil = n / sum(n))sigma <= 20000 <lgl> | n <int> | Anteil <dbl> |
|---|---|---|
| FALSE | 4000 | 1 |
Oder eleganter:
m2tab %>%
summarise(Anteil = mean(sigma <= 20000))Anteil <dbl> |
|---|
| 0 |
Die Wahrscheinlichkeit, dass Streuung kleiner oder gleich 20000 Dollar ist, liegt laut dem Modell bei 0 Prozent.
7.2.4 Aufgabe 2 e)
Zwischen welchen Häuserpreisen befindet sich das mittlere Intervall, dass 90 Prozent der möglichen Durchschnittspreise umfasst?
m2tab%>%
select(mean)%>%
eti(ci = .90)Parameter <chr> | CI <dbl> | CI_low <dbl> | CI_high <dbl> |
|---|---|---|---|
| mean | 0.9 | 66295.1 | 69988.95 |
Laut dem Modell werden die Grenzen des 90-Prozent-ETIs durch die Werte 66295.10 und 69988.95 gebildet.
7.3 Codesammlung
Generalisiertes lineares Modell aufstellen für den mittleren Wert der AV:
m <- stan_glm(AV ~ 1, data = data, refresh = 0)Modell als Tabelle ausgeben:
mtab <-
m1%>%
as_tibble()%>%
rename(mean = `(Intercept)`)Streuung & Mittelwert des Modells visualiseren
ggplot(mtab, mapping = aes(x = mean))+
geom_density()
ggplot(mtab, mapping = aes( x = sigma))+
geom_density()Wie groß ist die Wahrscheinlichkeit dafür, dass der mittlere Werte der Av nicht größer ist als X
mtab%>%
count(mean <= X)%>%
mutate(Anteil = n / sum(n))
#ODER
mtab %>%
summarise(Anteil = mean(mean <= X))Welche Streuung wird mit einer Wahrscheinlichkeit von X Prozent nicht überschritten?
mtab%>%
summarise(quantX = quantile(sigma, prob = .X))Wie groß ist die Wahrscheinlichkeit, dass die Streuung der AV bei X oder weniger liegt?
mtab%>%
count(sigma <= X)%>%
mutate(Anteil = n / sum(n))
#ODER
mtab %>%
summarise(Anteil = mean(sigma <= X))