4 Verteilungen
4.1 Achtung
Dadurch dass die Modelle bzw. Normalverteilungen bei jeder Durchführung neu simuliert werden, unterscheiden sich die simulierten Werte jedes Mal minimal. Unter Umständen führt dies zu leichten Abweichungen in den Dezimalstellen der Ergebnisse.
4.2 Aufgabe 1
4.2.1 Aufgabe 1 a)
Erstellen Sie eine Normalverteilung in R mit einem Mittelwert von 175 und einer Standardabweichung von 10. Nennen Sie diese Verteilung “Größe”. Simulieren Sie hunderttausend Fälle.
set.seed(42)
Größe <-
tibble(#Erstelle eine Tabelle
Verteilung = rnorm(#Erstelle mit rnorm eine Normalverteilung
1e5,#Insgesamt soll diese Verteilung Hunderttausend Werte haben
mean = 175,#Mittelwert dieser Menge sind 175 Zentimeter
sd = 10))#Die Werte streuen mit einer Standardabweichung von 10 Zentimetern4.2.2 Aufgabe 1 b)
Stellen Sie diese Verteilung graphisch dar.
ggplot(Größe, mapping = aes(x = Verteilung))+
geom_density()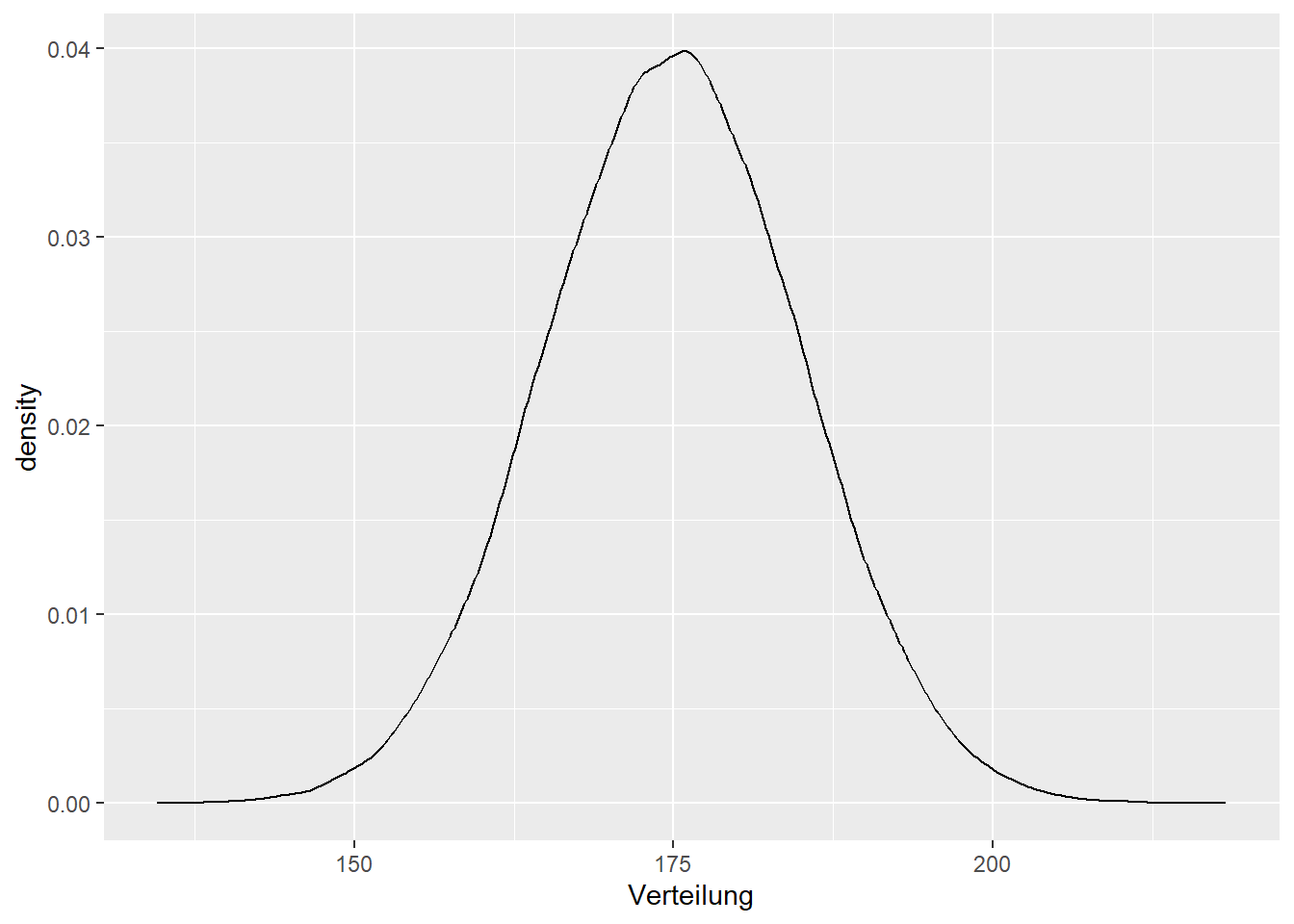
4.2.3 Aufgabe 1 c)
Wie viele Menschen haben eine Körpergröße unter 175? Wie groß ist dieser Anteil in Prozent?
Größe%>%
filter(Verteilung < 175)%>%
count()Es liegen rund 50000 Werte unterhalb von 175. Das heißt, von der Gesamtzahl an Menschen, die in der Verteilung erfasst worden sind, sind 50000 von 100000 kleiner als 175. Das entspricht 50 %.
4.2.4 Aufgabe 1 d)
Wie groß ist der Anteil an Menschen in der Verteilung, der größer ist als 150 Zentimeter?
Größe%>%
filter(Verteilung > 150)%>%
count()In dieser Verteilung sind ungefähr 99500 Personen, also ein Anteil von 99,5% größer als 150.
4.2.5 Aufgabe 1 e)
Wenn wir aus der Stichprobe irgendeine Person nehmen… Wie groß ist dann die Wahrscheinlichkeit, dass sie zwischen 165 und 185 groß ist?
Größe%>%
filter(Verteilung > 165)%>%
filter(Verteilung < 185)%>%
count()Die Menge an Menschen mit einer Körpergröße zwischen 165 und 185, liegt bei rund 68000. Das heißt, aus den 100000 erwischen wir mit einer Wahrscheinlichkeit von 68 % einen Menschen, der innerhalb der ersten Standardabweichung (175 +- 10) liegt.
4.2.6 Aufgabe 1 f)
Wie groß ist die Wahrscheinlichkeit eine Person zu erwischen, die mit ihrer Größe mindestens zwei Standardabweichungen über dem Durchschnitt liegt?
Eine Person die mindestens zwei Standardabweichungen über dem Durchschnitt liegt… Wir haben einen Durchschnitt von 175 und eine Standardabweichung von 10. Das heißt, wir brauchen jemanden, der mindestens 195 groß ist (Größe >= 175 + 10 + 10).
Eine Person die mindestens zwei Standardabweichungen über dem Durchschnitt liegt… Wir haben einen Durchschnitt von 175 und eine Standardabweichung von 10. Das heißt, wir brauchen jemanden, der mindestens 195 groß ist (Größe >= 175 + 10 + 10).
Größe%>%
filter(Verteilung >= 195)%>%
summarise(Anteil = 100*(n() / 100000))Ein Anteil von fast 2 Prozent ist größer als 195.
4.2.7 Aufgabe 1 g)
In welchem Intervall liegen grob 95% aller Werte?
Für normalverteilte Populationen gilt: Innerhalb der ersten Standardabweichung, also in unserem Fall 175 +- 10, liegen rund 68 % aller Werte. Innerhalb der zweiten Standardabweichung grob 95 % aller Werte. Innerhalb der dritten liegen 99.7 % aller Werte. Für uns bedeutet das, dass der Wertebereich zwischen 155 und 195 95 % aller Werte enthält.
Größe%>%
filter(Verteilung >= 155 & Verteilung <= 195)%>%
count()Wir sehen, dass tatsächlich ungefähr 95.000 Werte im vermuteten Intervall liegen. Ein Beleg dafür, dass es sich um ein 95-Prozent-Intervall handeln muss.
4.2.8 Aufgabe 1 h)
Überlegen Sie sich drei Beispiele für Variablen, die man in einer Normalverteilung darstellen kann und simulieren Sie sie in R.
Körpergewicht in Kg:
Gewicht<-
tibble(Verteilung = rnorm(1e5,
mean = 70,
sd = 10))
ggplot(Gewicht, mapping = aes(x = Verteilung))+
geom_density()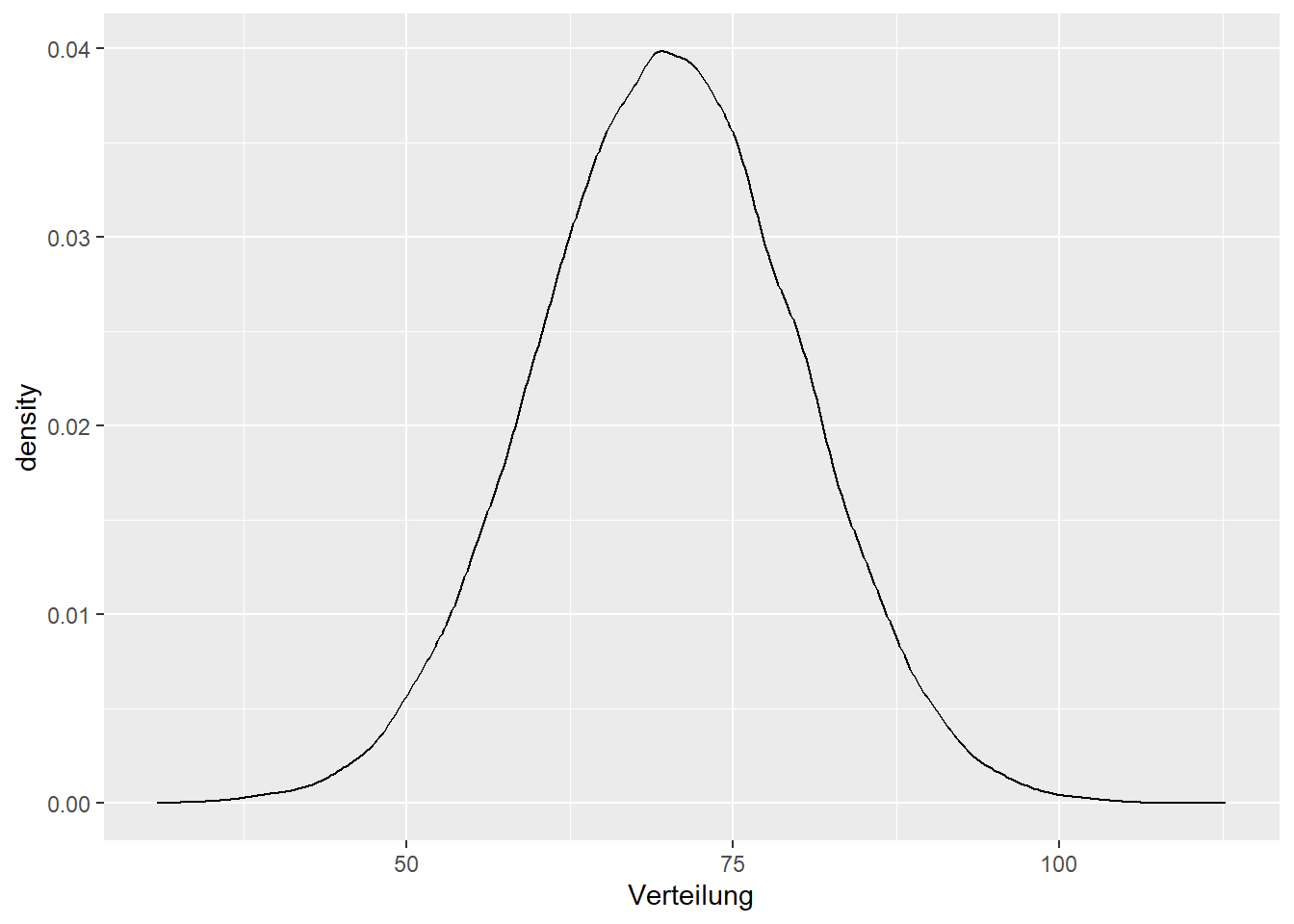
Distanz zum Arbeitgeber in km:
Distanz <-
tibble(Verteilung = rnorm(1e5,
mean = 20,
sd = 5))
ggplot(Distanz, mapping = aes(x = Verteilung))+
geom_density()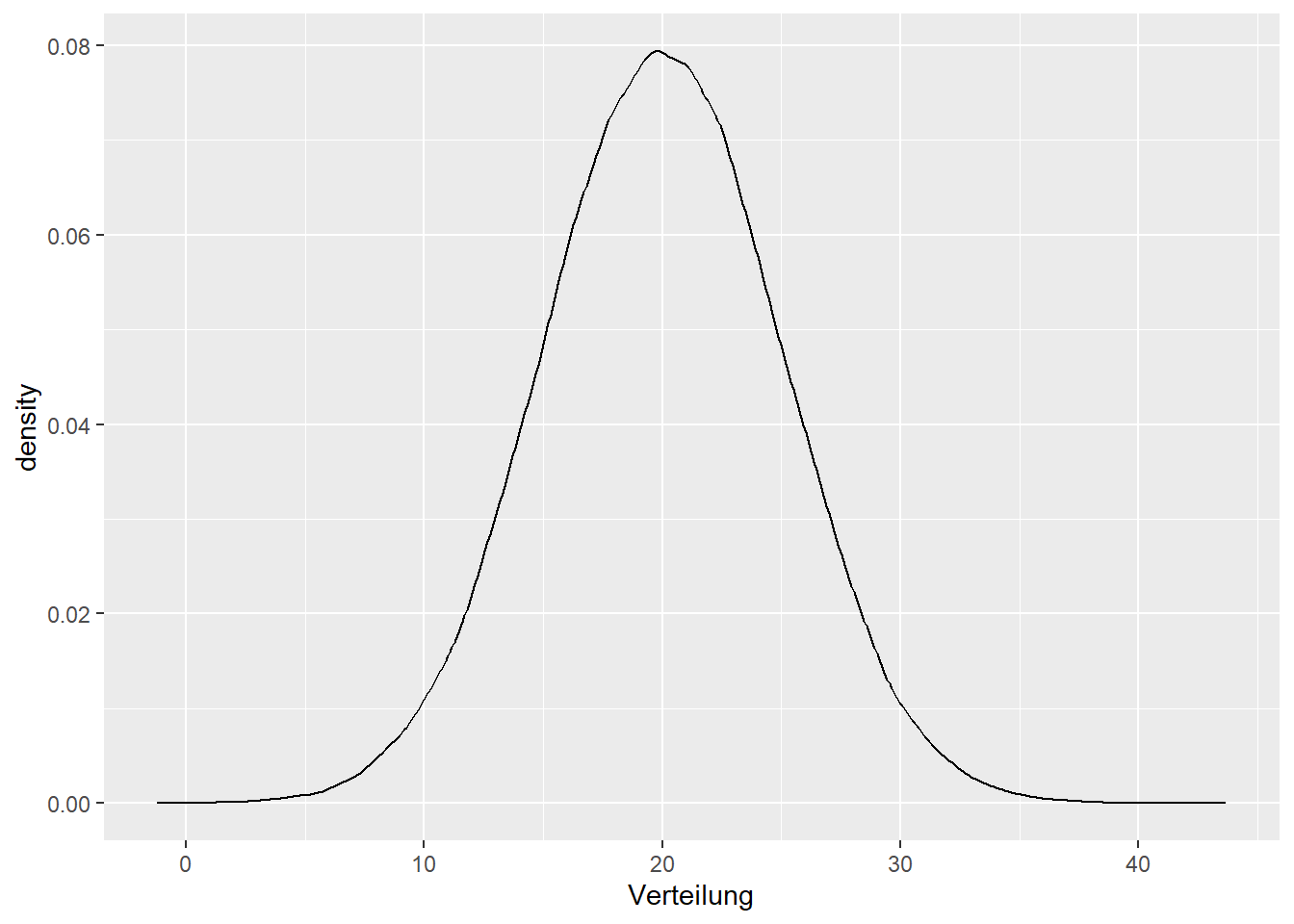
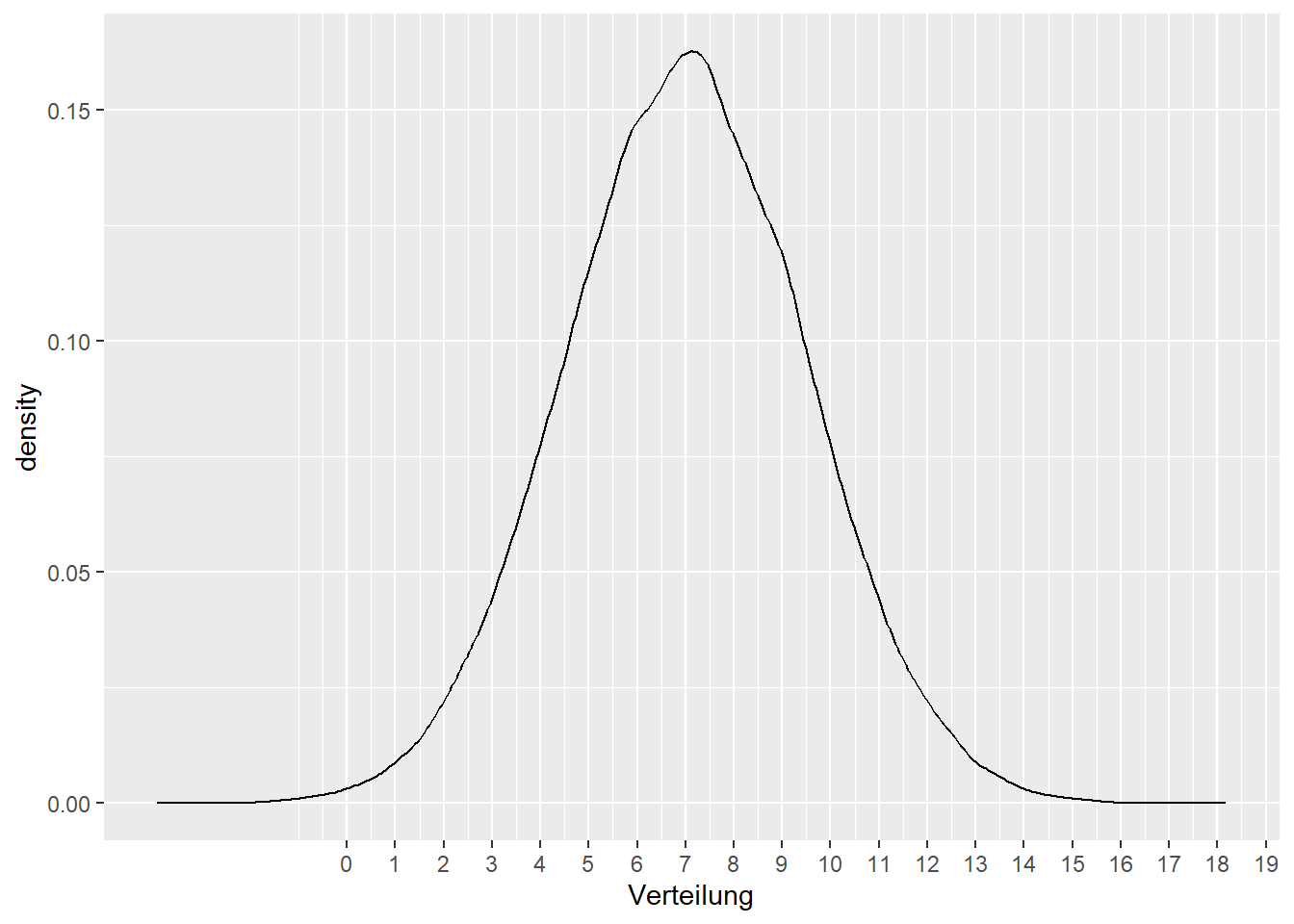
Wartezeit an Bushaltestellen in Minuten:
Zeit<-
tibble(Verteilung = rnorm(1e5,
mean = 7,
sd = 2.5))
ggplot(Zeit, mapping = aes(x = Verteilung))+
geom_density()+
scale_x_continuous(breaks = 0:20)- 1
- Nehmen wir an, dass Menschen an Bushaltestellen im Durchschnitt sieben Minuten warten
- 2
- Jedoch wartet der größte Teil nicht genau sieben, sondern zwischen viereinhalb bis neuneinhalb Minuten
- 3
- Zeige auf der x-Achse in jede einzelne Minute an
4.3 Aufgabe 2
4.3.1 Aufgabe 2 a)
Erstellen Sie eine Tabelle, in der eine Spalte anhand von 10000 Fällen zeigt, wie lange ein deutsches Auto im Durchschnitt fahrtauglich ist. Nehmen wir dafür an, dass die mittlere Dauer dafür 12 Jahre ist, aber diese Zahl eine Streuung von 2,5 Jahren hat.
set.seed(42)
PKW_Dauer <-
tibble(Dauer =
rnorm(1e4,
mean = 12,
sd = 2.5))4.3.2 Aufgabe 2 b)
Wie groß ist die Wahrscheinlichkeit, dass ein deutsches Auto eine unterdurchschnittliche Haltbarkeit aufweist?
PKW_Dauer%>%
filter(Dauer < mean(Dauer))%>%
summarise(Wahrscheinlichkeit = 100 * n()/1e4)- 1
- Filtere die Werte, die kleiner sind als der Durchschnitt der Spalte “Dauer”
- 2
- Wenn wir den Anteil der verbliebenen Autos mit 100 multiplizieren, dann errechnen wir so einen Prozentsatz
4.3.3 Aufgabe 2 c)
Wie groß ist die Wahrscheinlicheit, dass ein deutsches Auto zwischen 20 und 21 Jahre lang fahrtauglich ist?
PKW_Dauer%>%
filter(Dauer > 20 & Dauer < 21)%>%
summarise(Wahrscheinlichkeit = 100 * n()/1e4)4.3.4 Aufgabe 2 d)
Welches Betriebsjahr erreichen 84 % der Autos nicht mehr?
Diese Frage möchte wissen, unterhalb von welchem Wert 84 % aller anderen Werte liegen. Eine Möglichkeit wäre, die Tabelle zu öffnen und aufsteigend zu ordnen. Dann schauen wir, welcher Wert bei der Beobachtung 8400 angegeben ist (8400 von 10000 = 84 %). Da wir aufsteigend geordnet haben, müssen 84 % der Werte kleiner sein, als der, der bei 8400 angegeben ist.
Laut der Tabelle ist dieser Wert rund 14,5. Das heißt 84 % der deutschen Wägen gehen innerhalb der ersten vierzehneinhalb Jahre kaputt.
ODER wir nutzen die Quantilfunktion:
Die Quantilfunktion macht in einfache Worten gefasst folgendes: Sie nimmt einen Anteil einer Verteilung (z.B. 84 %) und schneidet die Verteilung genau an diesem Punkt ab. D.h. sie zeigt den Wert, der größer ist als 84 aller anderen Werte, aber kleiner ist als die übrigen 16 %. Somit bildet man das ein 84-Prozent-Quantil.
PKW_Dauer%>%
summarise(quan84 = quantile(Dauer, prob = .84))4.3.5 Aufgabe 2 e)
Welche Haltbarkeit wird mit einer Wahrscheinlichkeit von 95 % nicht überschritten?
PKW_Dauer%>%
summarise(quan95 = quantile(Dauer, prob = .95))4.3.6 Aufgabe 2 f)
In welchem Intervall liegen 90 % aller Werte?
PKW_Dauer%>%
summarise(quan5 = quantile(Dauer, prob = .05))PKW_Dauer%>%
summarise(quan95 = quantile(Dauer, prob = .95))95 % der Autos werden ca. zwischen 8 und 16 Jahre alt.
4.4 Codesammlung
Normalverteilung erstellen
normalv <-
tibble(
Verteilung = rnorm( #erstelle mit rnorm eine Normalverteilung in R
1e5, #insgesamt soll diese Verteilung Hunderttausend Werte haben
mean = x, #Mittelwert dieser Menge
sd = x)) #die Werte streuen mit einer Standardabweichung von xWie viele Fälle liegen unter einem bestimmten Wert?
normalv%>%
filter(Verteilung < x)%>%
count()Wie viele Fälle liegen zwischen zwei Werten?
normalv%>%
filter(Verteilung > x & Verteilung < y)%>%
count()Wie groß ist die Wahrscheinlichkeit, einen Fall zu erwischen, die über dem Wert X liegt?
normalv%>%
filter(Verteilung > X)%>%
summarise(Anteil = 100*(n() / 100000)) #um die Wahrscheinlichkeit direkt in Prozent zu bekommen yeahWelchen Wert erreichen x Prozent der Werte nicht mehr?
normalv%>%
summarise(quanX = quantile(Verteilung, prob = .X))